Version: 5.2.1
Least Squares: fitting a line to a sequence of 2d-points
Danny Yoo <[email protected]>
| (require (planet dyoo/least-squares:1:=0)) |
This is a simple implementation of the least squares method for lines, described in a standard statistics textbook.
Sample usage:
> (require (planet dyoo/least-squares))
> (least-squares '((0 -0.2342) (1 1.0001) (2 1.82123) (3 3.1415926)))
1.0948507800000002
-0.2100955200000003
> (define my-linear-function (least-squares-function '((0 -0.2342) (1 1.0001) (2 1.82123) (3 3.1415926))))
> (my-linear-function 0) -0.2100955200000003
> (my-linear-function 1) 0.8847552599999999
> (my-linear-function 2) 1.9796060400000002
> (my-linear-function 3) 3.0744568200000004
A slightly larger example:
> (define data '(#(2.745 2.08) #(2.7 2.045) #(2.69 2.05) #(2.68 2.005) #(2.675 2.035) #(2.67 2.035) #(2.665 2.02) #(2.66 2.005) #(2.655 2.01) #(2.655 2.0) #(2.65 2.0) #(2.65 2.005) #(2.645 2.015) #(2.635 1.99) #(2.63 1.99) #(2.625 1.995) #(2.625 1.985) #(2.62 1.97) #(2.615 1.985) #(2.615 1.99) #(2.615 1.995) #(2.61 1.99) #(2.59 1.975) #(2.59 1.995) #(2.565 1.955)))
> (least-squares data)
0.6420980926449493
0.30773474113939825
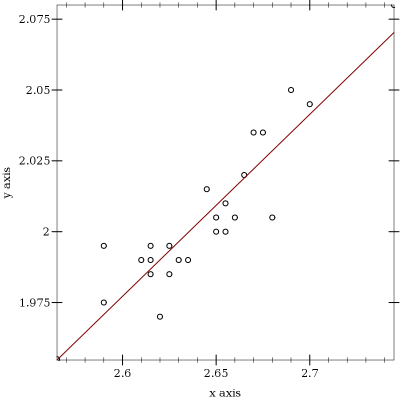
> (require plot)
> (plot (list (points data) (function (least-squares-function data))))
(least-squares data) →
[slope number] [intersect number] data : (sequenceof (sequence number number))
Computes the slope and intersect for a line that best
fits the points according to the method of least squares.
For example:
> (least-squares '((1 2) (3 4) (5 6)))
1
1
> (least-squares '((2.718 3.1415926) (1.618 1.414213)))
1.5703450909090884
-1.1266053570909036
(least-squares-function data) → [f (number -> number)] data : (sequenceof (sequence number number))
Constructs a function that fits the given data.
For example:
> (define g (least-squares-function '((2.718 3.1415926) (1.618 1.414213))))
> g (least-squares-function 1.5703450909090884 -1.1266053570909036)
> (g 0) -1.1266053570909036
> (g 1) 0.44373973381818477
> (g 2) 2.014084824727273
> (g 3) 3.584429915636362
The function returned from least-squares-function is actually a structured
value whose slope and intersect can be queried with least-squares-function-slope and
least-squares-function-intersect.
(least-squares-function-slope f) → number f : least-squares-function?
(least-squares-function-intersect f) → number f : least-squares-function?
Example:
> (define h (least-squares-function '((2.718 3.1415926) (1.618 1.414213))))
> (least-squares-function-slope h) 1.5703450909090884
> (least-squares-function-intersect h) -1.1266053570909036
(least-squares-function? x) → boolean x : any
Returns true if x is a function produced by least-squares-function.
Example:
> (least-squares-function? (lambda (x) x)) #f
> (define k (least-squares-function '((0 0) (1 1))))
> (least-squares-function? k) #t